La modulazione CSS consiste in una variazione lineare in frequenza, denominata chirp, che spazia nell’intera banda assegnata al canale (tipicamente 125, 250 o 500 KHz) e descritta dalla seguente relazione:
s(t)=a(t)cos[ø(t)]
dove
a(t)= Costante per 0<t<T; 0 altrove
T è la durata del chirp. La frequenza istantanea è definita come:
f(t)=(1/2π)*dθ/dt .
La velocità con cui cambia la frequenza è indicata anche come symbol rate
Rs(t)=d2f(t)/dt2 (2)
Nel caso di LoRa la variazione di frequenza è lineare, quindi la fase varia con legge quadratica e Rs è costante nel tempo. Nella modulazione CSS un simbolo[Nota 1] è indicato anche con il termine chirp. Il chirp rate coincide con la frequenza di simbolo, il numero di simboli trasmessi in un secondo.
L’escursione lineare di frequenza del chirp può essere anche scritta come
f(t)=fC-B/2+µ *(B/T)*t per 0<t<T (3)
dove T è la durata del chirp, B è la banda del canale di comunicazione, fc è la frequenza della portante (centrata in B), m è la velocità di variazione della frequenza. Di seguito m assume i valori
- µ=1, la frequenza sale nel tempo, up-chirp;
- µ=-1 la frequenza decresce nel tempo, down-chirp.
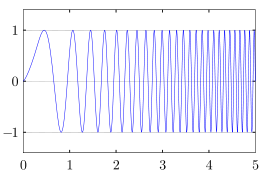
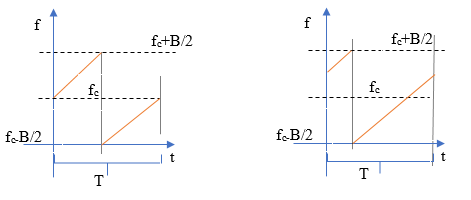
In Figura 1 è illustrato il segnale di up-chirp nel dominio del tempo. In Figura 2 sono riportati i segnali di up-chirp e down-chirp nel dominio delle frequenze.

LoRa(link is external) definisce il parametro SF (Spreading Factor) che corrisponde alla dimensione in bit del simbolo. Lo spreading factor caratterizza diversi parametri della comunicazione LoRa.
Un simbolo corrisponde ad una escursione di frequenza che copre la banda B nel tempo T. Il symbol rate è
Rs= 1/T= B/2SF (4)
Ogni simbolo è composto da SF bit, per cui il bit rate vale
Rb=SF*Rs=SF*B/2SF
Il bit rate effettivo del dato trasmesso è inferiore a Rb in quanto la modulazione LoRa prevede bit aggiuntivi per funzioni di header e correzione di errori.
LoRa ammette valori di Spreading Factor che variano da 7 a 12. Con uno specifico SF si hanno 2SF simboli possibili. Detto S il generico simbolo, S={0,…, 2SF-1}, l’intera Banda B è suddivisa in chip (attenzione, non chirp) pari al numero di simboli: 2SF chip. Per rappresentare uno specifico simbolo S, la escursione del segnale modulato, inizia con una frequenza di chip fc-B/2 +SB/2SF al raggiungimento del limite superiore pari a fc+B/2, la frequenza cambia istantaneamente al valore fc-B/2 e continua a crescere fino a fc-B/2 +SB/2SF . L’intera escursione ha durata T. La codifica del simbolo è fisicamente ottenuta variando la frequenza iniziale del segnale ad ogni chirp mantenendo la continuità della fase.
Il chip rate è Rc= Rs*2SF. Graficamente, e in modo indicativo, il comportamento è riportato in Figura 3.
fC-B/2+SB/2SF+t*B/T per 0≤t<T(1-S/2SF) e
fc-B/2+ t*B/T per (1-S/2SF≤t<T)
In Figura 4 sono mostrati una serie di simboli trasmessi con modulazione CSS. I rettangoli rossi delimitano i singoli simboli

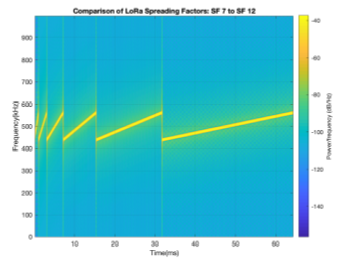
Il rapporto fra il symbol rate e il bit rate è proporzionale allo spreading gain [50] Rb/Rb=SF. Aumentando lo spreading factor diminuisce la pendenza della rampa. Ad ogni incremento di una unità dello SF corrisponde al raddoppio del tempo necessario a spedire il simbolo e a circa il dimezzamento del bit rate (Eq. 5 ). In Figura 5 è mostrato il chirp al variare del parametro SF.
Alla diminuzione del bit rate corrisponde un aumento della massima distanza di trasmissione, a parità di potenza. Nel caso particolare di LoRa, sono presenti ulteriori manipolazioni utili a formare un livello fisico (PHY layer) robusto. Ad ogni bit trasmesso sono aggiunti bit usati per la correzione di errore, FEC (Forward Error Correction). Con la correzione di errore, il ricevitore è in grado di determinare se il dato ricevuto è corrotto e, entro certi limiti, correggere l’errore, evitando la ritrasmissione del dato.
Lo schema di correzione adottato in LoRa è variabile in funzione del parametro denominato coding rate CR che può assumere valore da 1 a 4. Ad ogni 4 bit trasmessi sono associati CR bit per la correzione di errore. In questo modo, pur aumentando i bit trasmessi rispetto ai dati realmente utili, si aumenta la robustezza complessiva della comunicazione, riducendo le ritrasmissioni in caso di errore. Il miglioramento ottenuto è indicato con il termine coding gain.
Il bit rate utile, modificato per la presenza del meccanismo FEC, è il seguente:
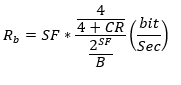
Il rapporto 4/4(+CR) è spesso indicato con notazione 4/n con n = 5, .. , 8.
Tutti i meccanismi di miglioramento della qualità di trasmissione (spreading gain, coding gain, ecc.) concorrono a formare il processing gain(link is external).
L’LoRa Modem(link is external) indica valori di process gain di 20dB per SF=12 e 15dB per SF=10. Il process gain rientra nel calcolo del link budget per stimare la massima distanza possibile della trasmissione.
I dati subiscono ulteriori trasformazioni quali Data whitening(link is external) e gray indexing. Sono operazioni che consistono nel riposizionamento dei bit oggetto della trasmissione in una forma pseudocasuale, utili a garantire l’uso efficiente dell’intera banda e limitare sequenze di bit uguali, che pregiudicano le operazioni di sincronizzazione a lato ricevitore. I dettagli di queste trasformazioni sono proprietari, tipici di LoRa e sono soggetti a brevetti di proprietà Semtech e noti solo a grandi linee.
La Demodulazione del simbolo(link is external), in LoRa, inizia con un processo denominato dechirping. Il segnale ricevuto, traslato in frequenza (banda base), viene moltiplicato con il complesso coniugato di un chirp generato localmente, avente lo stesso SF del segnale ricevuto e con la stessa banda B. Il risultato del prodotto è una sinusoide la cui frequenza corrisponde alla frequenza dello scostamento (in chips SB/2SF ) del segnale modulato, frequenza valutata con tecniche numeriche FFT (Fast Fourier Transform) per risalire al simbolo S ricevuto. Il chirp generato localmente nel ricevitore deve seguire l’equivalente generato nel trasmettitore. Per consentire la sincronizzazione il trasmettitore invia un preambolo iniziale.
La Figura 46 riporta la struttura del pacchetto LoRa:

Preambolo: è una sequenza nota di up-chirp e down-chirp. LoRaWAN regional parameters(link is external) richiede un preambolo di 8 up-chirp iniziali seguiti da 2.25 down-chirp.
Header (opzionale): contiene la lunghezza del payload, il data rate, l’eventuale presenza del CRC nel payload.
Lo header ha Code Rate fisso CR=4/8. LoRaWAN richiede header esplicito
Header CRC: 1 byte CRC LoRaWAN richiede CRC (Cyclic Redundancy Check) nei messaggi down link, ma non nei messaggi di up link (da gateway a nodo).
Payload: il dato da trasmettere. Ha il Code Rate definibile. La struttura dettagliata del payload è definita dal MAC (Media Access Control) e interessa i livelli superiori al livello fisico.
In Figura 47 un frame LoRa completo di preambolo.

La dimensione del payload può variare con un massimo di 255 byte. L’uso di bande libere è regolato dalla legislazione vigente nelle varie regioni, ma in quasi tutti i casi è richiesto un duty-cycle. Questo limita il tempo di trasmissione (air-time) e di conseguenza la lunghezza massima del payload.
Si deve considerare, inoltre, la possibilità di regolazione dinamica dello SF (ADR Adaptive Data Rates), in relazione alla qualità del segnale ricevuto. Aumentando lo SF il tempo di trasmissione aumenta e obbliga a diminuire la dimensione del payload al valore consentito dal massimo SF.
Nell’ambito di una rete LoRaWAN, il gestore può imporre ulteriori restrizioni per il traffico di up-link e di down-link.
In Tabella 1 i limiti di bit rate e payload size:

[1] Il simbolo è l’unita di informazione elementare trasmessa nel canale di comunicazione. Ad ogni differente simbolo corrisponde una variazione significativa del segnale modulato. L’insieme dei possibili (S) simboli formano l’alfabeto. In binario, S simboli sono rappresentabili con N bit: S=2N. https://en.wikipedia.org/wiki/Symbol_rate#Symbols(link is external)

Commenti recenti